Tóm tắt đề bài: Cho đồ thị vô hướng (cây) ~G = (V,E),|V| = n,|E| = n-1~. Tìm đường đi (mỗi đỉnh đi qua đúng một lần) có tích số nhỏ nhất, với tích số của đường đi được tính bằng tích trọng số các nút của đường đi chia số nút trên đường đi.

Ta sẽ tạm gọi các đỉnh có trọng số ~1~ là đỉnh ~a~, và các đỉnh có trọng số lớn hơn ~1~ là đỉnh ~b~. Ta nhận thấy rằng đường đi tối ưu nhất chỉ chứa tối đa ~1~ đỉnh ~b~.

Nếu ~G~ không có đỉnh ~a~, đường đi có tích số nhỏ nhất cần tìm chỉ có một đỉnh ~b~ với giá trị trọng số nhỏ nhất. Ngược lại, đường đi cần tìm thuộc vào một trong hai dạng theo thứ tự duyệt:

• Dạng ~1~: Đường đi bao gồm ~k~ đỉnh ~a~, tích số ~P = \frac{1}{k}~.

• Dạng ~2~: Đường đi bao gồm ~k_1~ đỉnh ~a~, một đỉnh ~b~ và ~k_2~ đỉnh ~a~, tích số ~P = \frac{b}{k_1+k_2+1}~

Ta dễ dàng suy ra rằng để tìm được phương án tối ưu, ta cần đi qua càng nhiều đỉnh ~a~ càng tốt.

Xét ví dụ sau như hình vẽ ~1~:

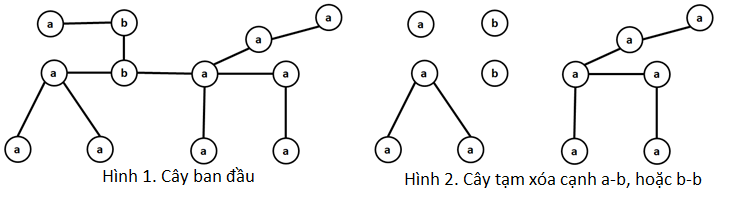
Với dạng thứ nhất, ta chỉ đi qua các đỉnh ~a~, vì vậy ta có thể biến đổi ~G~ bằng cách tạm thời xóa đi những cạnh nối ~a-b~ hoặc ~b-b~. Ta có hình vẽ ~2~.

Do ~G~ có đúng ~n-1~ cạnh nên ~G~ bị chia thành các thành phần liên thông (cây con), với ví dụ trên ta sẽ tạm gọi các thành phần liên thông (cây con) chỉ chứa đỉnh ~a~ là: cây ~1~, cây ~3~ và cây ~6~ (tương ứng với số đỉnh).

Lúc này, đường đi chỉ có thể thuộc một trong các cây con. Với mỗi cây con, số đỉnh ~a~ nhiều nhất có thể đi qua chính là đường kính của cây đó (Các bạn có thể tham khảo định nghĩa, tính chất và thuật toán tìm đường kính tại đây).

Ta dễ dàng có được ~k~ bằng độ dài đường kính lớn nhất trong số các cây con. Trong ví dụ trên, ~k = 5~ là đường kính của cây ~6~.

Sau khi có được thuật toán cho dạng thứ nhất, ta có thể đưa ra được ý tưởng cho dạng đường đi thứ hai: Kết nối hai cây con thông qua một "khớp nối" là đỉnh ~b~.

Mỗi đỉnh ~b~ là "khớp nối" nếu có cạnh nối với ~m~ đỉnh ~a~ (~m \geq 2~). Vì ~G~ có số cạnh ~|E| = n - 1~ nên đỉnh ~b~ kết nối ~m~ cây con. Đường đi dạng thứ hai bao gồm đỉnh ~b~ và hai nhánh thuộc hai trong số ~m~ cây con.

Trong ví dụ trên, đường đi dạng thứ hai tối ưu nhất có tích số ~P = \frac{b}{2+3+1}~, trong đó có hai đỉnh ~a~ thuộc cây con ~3~ và ba đỉnh ~a~ thuộc cây con ~6~.

Vậy tóm lại, ta cần làm như sau:

• Tìm các cây con chỉ chứa đỉnh ~a~.

• Tìm đường kính lớn nhất trong số các cây con để tối ưu đường đi dạng thứ nhất.

• Duyệt qua với mỗi đỉnh ~b~, tìm hai nhánh có độ dài lớn nhất để tối ưu đường đi dạng thứ hai.

Kết quả là giá trị tích số nhỏ nhất trong hai dạng đường đi.

Độ phức tạp: ~\mathcal{O}(n)~. Code tham khảo