Định lý: Đồ thị đầy đủ ~K_n~ với ~n \geq 3~ và ~n~ lẻ có đúng ~\frac{n - 1}{2}~ chu trình Hamilton phân biệt.

Chứng minh: ~K_n~ có ~\frac{n(n - 1)}{2}~ cạnh và mỗi chu trình Hamilton có ~n~ cạnh, nên số chu trình phân biệt nhiều nhất là ~\frac{n - 1}{2}~.

Cách vẽ: Giả sử các đỉnh của ~K_n~ là ~1, 2, \ldots, n~. Đặt đỉnh ~1~ tại tâm của một đường tròn và các đỉnh còn lại đặt cách đều nhau trên đường tròn (mỗi cung là ~\frac{360^o}{n - 1}~) sao cho đỉnh lẻ nằm ở nửa đường tròn trên và đỉnh chẵn nằm ở nửa đường tròn dưới. Ta có ngay chu trình Hamilton đầu tiên là ~1, 2, \ldots, n, 1~.

Các đỉnh giữ cố định, xoay khung theo chiều kim đồng hồ với góc quay lần lượt: ~\frac{360^o}{n - 1}, 2 \times \frac{360^o}{n - 1}, \ldots, \frac{n - 3}{2} \times \frac{360^o}{n - 1}~ ta có tổng ~\frac{n - 1}{2}~ chu trình Hamilton phân biệt.

Ví dụ xét đồ thị ~K_9~, ta có các chu trình Hamilton cần tìm như hình vẽ sau:

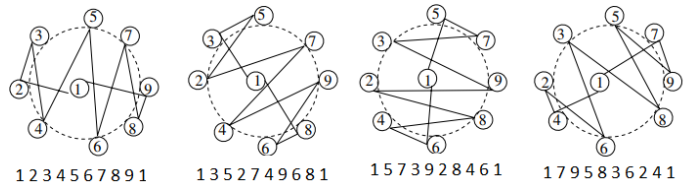
Các Anh Chị giỏi thuật toán cài đặt định lý trên giúp Bi.

Input

Dòng đầu tiên là số nguyên dương ~T~ thỏa ~T \le 10~ là số testcase

~T~ dòng tiếp theo mỗi dòng chứa số nguyên dương ~n~ thỏa ~3 \le n \le 19~, ~n~ lẻ.

Output

Ứng với mỗi testcase in ra các chu trình Hamilton phân biệt cần tìm, mỗi testcase cách nhau một dòng trắng.

Samples

Sample Input 1

2
3
5

Sample Output 1

1 2 3 1

1 2 3 4 5 1
1 3 5 2 4 1