Home - ITLab Code Runner

Blog
Events

Hello World!

admin posted on June 12, 2023, 5:00 a.m. 2

Chào mừng đến với coder.husc.edu.vn

Sau một thời gian dài (2017-2023) chúng ta cùng nhau học và thi lập trình trên oj.husc.edu.vn. Một web chấm bài dựa trên nền tảng Domjudge được hiệu chỉnh lại hầu hết các chức năng cho phù hợp với nhu cầu sử dụng. Chúng ta đã có được nhiều lợi ích cho việc học và thi lập trình nhất là các đội tuyển ICPC và OLP của Khoa.

Thuận theo xu thế chung và tiện hơn cho việc giao tiếp cộng đồng, nay chúng tôi xây dựng lại web chấm bài và đổi tên là coder.husc.edu.vn dựa trên nền tảng DMOJ. Các bài tập dạng cơ bản sẽ được đặt tên là Nhập môn lập trình dành cho sinh viên khoa Công nghệ Thông tin Đại học Khoa học Huế. Phần bài tập còn lại sẽ phân bố theo đúng chuẩn của các trang web lập trình, tức là gán nhãn cho từng kiểu bài tập và thể loại của chúng. Và để nghiêm túc các bài toán sẽ gán nhãn nguồn tham chiếu nếu sử dụng chúng.

Hy vọng các bạn sẽ có trải nghiệm mới, hiện nay chúng tôi đã xây dựng xong UI cho có tính riêng biệt hơn và đẹp hơn. Riêng các bạn hãy thực hiện phương châm sau:

do {
    train;      (* in joy *)
    practice;   (* in passion *)
    perform;    (* in love *)
} until (excellence);

Các bạn có thể làm các bài toán được public, ví dụ bài này dành cho bạn.

Review in round 7 Câu D

Yunan posted on Aug. 4, 2023, 9:09 a.m. 0

Tóm tắt đề bài

Bài toán sử dụng kĩ thuật ghép hình rất hay gặp trong các bài Dynamic Programming hình học. Ở cuối bài viết, mình giới thiệu một số bài toán tương tự sử dụng kĩ thuật này.

Cách tiếp cận 1: Duyệt qua tất cả tập con $S$ , tìm diện tích bao lồi và cập nhật kết quả. Lưu ý rằng $|S| \geq 3$ . Độ phức tạp $\mathcal{O}(2^n.nlogn)$ . Với giới hạn $n \le 80$ , thuật toán trên không tối ưu. Trước khi đến cách tiếp cận tối ưu hơn, ta có một số nhận xét như sau:

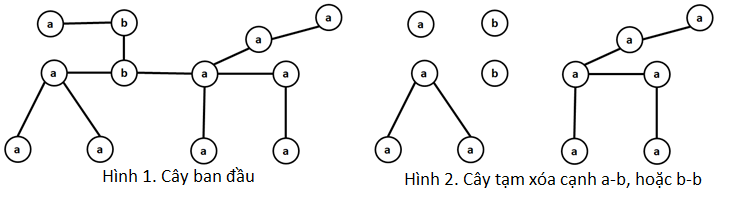
Nhận xét 1: Với các đỉnh tọa độ nguyên, diện tích đa giác (kể cả đa giác không lồi) có giá trị nguyên khi và chỉ khi hai lần diện tích đa giác là số chẵn (dễ dàng chứng minh với Pick’s theorem hoặc Shoelace formula).

Nhận xét 2: Với tập điểm $S$ , gọi $S_{on}$ là tập các điểm nằm trên bao lồi của $S$ và $S_{in}$ là tập các điểm nằm bên trong bao lồi của $S (S_{on} \cup S_{in} = S)$ . Gọi $S'$ là tập con của $S$ và $S'_{on}$ là tập các điểm nằm trên bao lồi của $S'$ . Khi đó số lượng tập $S'$ thỏa mãn $S_{on} = S'_{on}$ (bao lồi của $S$ và $S'$ trùng nhau) là $2^{|S_{in}|}$ . Ví dụ: Hình $1$ có $2^4 = 16$ tập $S'$ thỏa mãn $S_{on} = S'_{on}$ .

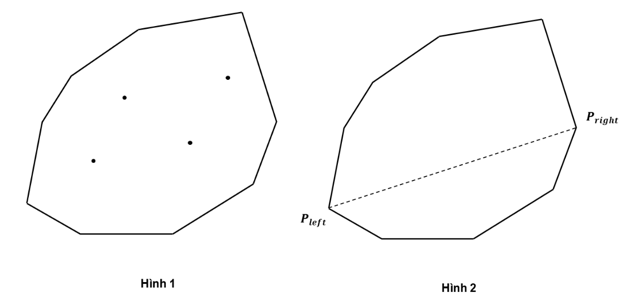
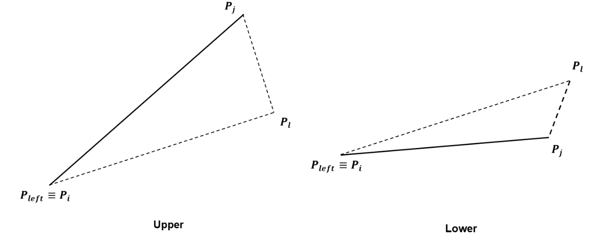
Nhận xét 3: Quan sát ở hình $2$ , gọi điểm có hoành độ $x$ nhỏ nhất là điểm trái nhất $P_{left}$ và điểm có hoành độ $x$ lớn nhất là điểm phải nhất $P_{right}$ . Từ đoạn thẳng nối hai điểm trên, ta có thể chia đa giác lồi thành hai phần: phần nửa trên (tạm gọi là Upper) gồm các điểm nằm phía trên đường nối và phần nửa dưới (Lower) gồm các điểm nằm phía dưới đường nối. Khi đó diện tích đa giác lồi bằng tổng diện tích hai phần nửa trên và nửa dưới: Convex_Area = Upper_Area + Lower_Area.

Cách tiếp cận 2: Quy hoạch động với kĩ thuật ghép hình:

Sắp xếp $n$ điểm theo thứ tự tăng dần hoành độ $x$ , nếu có cùng hoành độ $x$ , sắp xếp theo thứ tự tăng dần tung độ $y$ . Duyệt qua với mọi đỉnh $P_{left}$ , ta đếm số lượng tập điểm $S$ thỏa mãn yêu cầu đề bài và bao lồi của nó nhận điểm $P_{left}$ là điểm trái nhất (có hoành độ $x$ nhỏ nhất) với tư tưởng quy hoạch động như sau:

Gọi dp[z][i][j][k] với $0 \le z \le 1,left < j \le n,left \le i < j,0 \le k \le 1$ là số lượng tập $S$ thỏa mãn đồng thời các yêu cầu sau:

Bao lồi của nó nhận điểm $P_{left}$ là điểm trái nhất và $P_j$ là điểm phải nhất.
$z=0$ nếu $S$ là một Upper (mọi điểm thuộc tập $S$ nằm phía trên đường nối $P_{left}$ và $P_j$ ) và $z=1$ nếu $S$ là một Lower (mọi điểm thuộc tập $S$ nằm phía dưới đường nối $P_{left}$ và $P_j$ ).
Bao lồi của nó nhận điểm $P_i$ là điểm liền kề đứng trước điểm $P_j$ (khi duyệt bao lồi từ $P_{left}$ đến $P_j$ , hai điểm cuối cùng được duyệt tương ứng là $P_i$ và $P_j$ ).
Phần dư khi chia hai lần diện tích bao lồi của $S$ cho $2$ bằng $k$ ( $k = 0$ nếu hai lần diện tích là số chẵn và $k = 1$ nếu hai lần diện tích là số lẻ).

Cách tính dp[z][i][j][k] được mình họa ở $2$ hình sau:

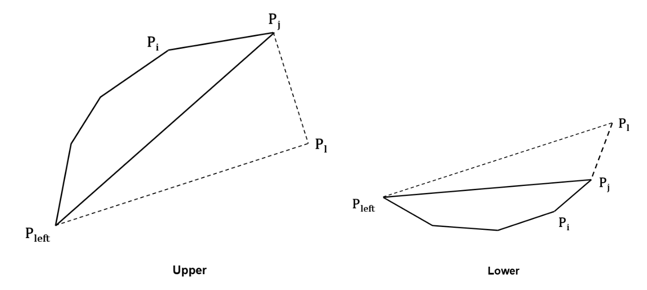
Tư tưởng ghép hình: Với đa giác lồi $\{P_{left},\ldots, P_i,P_j\}$ đã được tính toán, ta tiến hành ghép tam giác $\{P_{left}, P_j, P_l\}$ với $(j <l)$ để có được đa giác mới $\{P_{left},\ldots, P_j,P_l\}$ . Từ đó, ta có công thức quy hoạch động như sau:

$\displaystyle \begin{cases} dp[0][j][l][k \oplus parity[left][j][l]] = & \displaystyle\sum_{i=left}^{j-1}{(dp[0][i][j][k]} \times 2^{cnt[left][j][l]}) \text{ với } cw(P_{left}, P_i, P_j) \\ dp[1][j][l][k \oplus parity[left][j][l]] = & \displaystyle\sum_{i=left}^{j-1}{(dp[1][i][j][k]} \times 2^{cnt[left][j][l]}) \text{ với } ccw(P_{left}, P_i, P_j) \end{cases}$

Trong đó:

parity[a][b][c] = 0 nếu hai lần diện tích tam giác $\{P_a, P_b, P_c\}$ là số chẵn, ngược lại parity[a][b][c] = 1.
cnt[a][b][c] là số lượng điểm $P_i (1 \le i \le n)$ nằm bên trong tam giác $\{P_a, P_b, P_c\}$ .
$cw(P_a, P_b, P_c)$ nếu $3$ điểm $P_a, P_b, P_c$ theo thứ tự chiều kim đồng hồ và $ccw(P_a, P_b, P_c)$ nếu $3$ điểm $P_a, P_b, P_c$ theo thứ tự ngược chiều kim đồng hồ.

Các giá trị parity[a][b][c] và cnt[a][b][c] có thể tính toán trước trong $\mathcal{O}(n^4)$ .

Một số lưu ý trong công thức QHĐ trên:

Việc ta phải nhân với $2^{cnt[left][j][l]}$ đã được đề cập trong nhận xét 2.

Giới hạn của $i$ là $left \le i < j$ chứ không phải $left < i < j$ . Việc $i = left$ do Upper hoặc Lower có thể là một đoạn thẳng (đa giác chỉ có $2$ đỉnh). Minh họa ở $2$ hình:

Từ nhận xét 3, ta có kết quả của bài toán được tính theo công thức:

$\displaystyle \displaystyle\sum_{left=1}^{n}\Biggl( \sum_{j=left+1}^{n} \biggl( \sum_{k=0}^{1} \Bigl( \sum_{i=left}^{j-1}(dp[0][i][j][k]) \times \sum_{i=left}^{j-1}(dp[1][i][j][k])\Bigl) \biggl) \Biggl) -\displaystyle{n \choose 2}$

Lưu ý rằng ở đáp án, ta phải trừ đi số lượng tập $S$ với $|S|=2$ do ta đã đề cập về vấn đề Upper hoặc Lower có thể là một đoạn thẳng ở trên.

Mở rộng: Kĩ thuật ghép hình như trên được dùng ở hầu hết các bài toán QHĐ hình học, đặc biệt là hình học bao lồi. Để luyện tập kĩ thuật này, các bạn có thể tham khảo một số bài toán:

Empty Convex Polygons - vjudge : Bài toán theo mình khá hay vì thể hiện rõ việc sử dụng kĩ thuật “ghép hình” để tìm đa giác lồi rỗng (đa giác không có điểm nằm trong) có diện tích lớn nhất.
Polygon – codeforces : Mặc dù ở mức 3000* nhưng với việc áp dụng kĩ thuật “ghép hình” thì tư tưởng để giải bài toán này không quá khó.

Mã nguồn tham khảo

Review in round 5 Câu D

hazzu posted on July 20, 2023, 4:52 a.m. 0

Tóm tắt đề bài

Nhận xét đầu tiên: về mặt tính toán, đây là một bài toán số lớn và cần cài đặt Big Integer hoặc dùng Java, Python để lập trình.

Đường đi trong bảng là sự kết hợp của dạng đường đi cơ bản sau:

Từ đó, ta có thể sử dụng Dynamic Programming để giải quyết bài toán như sau:

Gọi $dp[i][type]$ là giá trị lớn nhất khi di chuyển trong bảng gồm $i$ cột đầu tiên và kết thúc bằng đường đi dạng $type$ với $type \in \{1, 2\}$
Cơ sở quy hoạch động:
- $dp[0][1] = -\infty$ .
- $dp[0][2] = 0$ .
Công thức truy hồi:
- $dp[i][type] = max(dp[j - 1][2 - type] * 2^{3(i - j + 1)} + cost_{type}[j][i])$ với $1 \le j \le i$ .
- Với $cost_{type}[j][i]$ là giá trị khi di chuyển theo đường đi dạng $type$ trong cột $[j..i]$ .
Đáp án bài toán là $max(dp[n][1], dp[n][2])$ .

Mã nguồn tham khảo

Review in round 4 Câu E

hazzu posted on July 15, 2023, 1:29 p.m. 0

Tóm tắt đề bài: Cho đồ thị vô hướng liên thông G = (V, E), |V| = n, |E| = m. Đồ thị G có ít nhất một cạnh cầu. Cho hai đỉnh s và t, tìm thời gian nhỏ nhất để đi từ (s, t) tới (u, v) với (u, v) là hai đỉnh của một cạnh cầu bất kỳ trong G.

Ban đầu, ta sử dụng thuật toán Dijkstra để tính đường đi ngắn nhất từ đỉnh s và đỉnh t tới các đỉnh còn lại trong G.

Sau đó, ta đi tìm tất cả các cạnh (u, v) là cầu của đồ thị G. Thời gian nhỏ nhất để đi từ (s, t) tới (u, v) được tính theo công thức sau :

t₁ = max(dist_s[u], dist_t[v])
t₂ = max(dist_s[v], dist_t[u])
time_{(u, v)} = min(t₁, t₂)

Đáp án là min(time_{(u, v)}) với (u, v) là cạnh cầu của G

Độ phức tạp: $\mathcal{O}(nlogn)$ . Code tham khảo

Review in round 4 Câu D

hazzu posted on July 14, 2023, 5:02 a.m. 0

Tham khảo đề bài:

Lời giải

Ta sắp xếp các đoạn $[l_i, r_i]$ theo chiều tăng dần $r_i$ .

Để tối ưu nhất, ta tham lam chọn các phần tử từ phải sang trái và chưa được chọn trước đó của đoạn $[l_i, r_i]$

Chứng minh:

Xét hai đoạn $[l_i, r_i]$ và $[l_j, r_j], (i < j)$ sau khi đã sắp xếp.

1) Trường hợp 1: $[l_i, r_i]$ giao $[l_j, r_j]$ $(l_j \leq r_i)$ :

Nếu ta chọn các phần tử thuộc đoạn $[l_j, r_i]$ thì thoả mãn được cùng lúc cả hai đoạn $[l_i, r_i]$ và $[l_j, r_j]$ .
Nếu ta chọn các phần tử thuộc nửa đoạn $[l_i, l_j)$ thì chỉ thoả mãn được đoạn $[l_i, r_i]$ mà không thoả mãn được đoạn $[l_j, r_j]$ .
Suy ra ưu tiên chọn các phần tử bên phải của đoạn $[l_i, r_i]$

2) Trường hợp 2: $[l_i, r_i]$ không giao $[l_j, r_j]$ ( $r_i < l_j$ ).

Trường hợp này, ta chọn phần tử nào trong đoạn $[l_i, r_i]$ thì chỉ thoả mãn được đoạn $[l_i, r_i]$ .

Các bước thực hiện liên tục từ đoạn $[l_1, r_1]$ tới đoạn $[l_n, r_n]$ như sau:

Nếu $|Z \cap [l_i, r_i]| < c_i$ thì tham lam chọn các phần tử từ phải sang trái và chưa được chọn trước đó của đoạn $[l_i, r_i]$ .
Nếu $|Z \cap [l_i, r_i]| \geq c_i$ thì xét tiếp đoạn $[l_{i+1}, r_{i+1}]$ .

Các thao tác tìm $|Z \cap [l_i, r_i]|$ và tham lam chọn phần tử có thể sử dụng Segment Tree và tìm kiếm nhị phân để giải quyết

Độ phức tạp: $\mathcal{O}(nlog^2n)$ . Code tham khảo

Review in round 1 Câu C

Yunan posted on June 26, 2023, 1:09 p.m. 0

Tóm tắt đề bài: Cho đồ thị vô hướng (cây) $G = (V,E),|V| = n,|E| = n-1$ . Tìm đường đi (mỗi đỉnh đi qua đúng một lần) có tích số nhỏ nhất, với tích số của đường đi được tính bằng tích trọng số các nút của đường đi chia số nút trên đường đi.

Ta sẽ tạm gọi các đỉnh có trọng số $1$ là đỉnh $a$ , và các đỉnh có trọng số lớn hơn $1$ là đỉnh $b$ . Ta nhận thấy rằng đường đi tối ưu nhất chỉ chứa tối đa $1$ đỉnh $b$ .

Nếu $G$ không có đỉnh $a$ , đường đi có tích số nhỏ nhất cần tìm chỉ có một đỉnh $b$ với giá trị trọng số nhỏ nhất. Ngược lại, đường đi cần tìm thuộc vào một trong hai dạng theo thứ tự duyệt:

Dạng $1$ : Đường đi bao gồm $k$ đỉnh $a$ , tích số $P = \frac{1}{k}$ .
Dạng $2$ : Đường đi bao gồm $k_1$ đỉnh $a$ , một đỉnh $b$ và $k_2$ đỉnh $a$ , tích số $P = \frac{b}{k_1+k_2+1}$

Ta dễ dàng suy ra rằng để tìm được phương án tối ưu, ta cần đi qua càng nhiều đỉnh $a$ càng tốt.

Xét ví dụ sau như hình vẽ $1$ :

Với dạng thứ nhất, ta chỉ đi qua các đỉnh $a$ , vì vậy ta có thể biến đổi $G$ bằng cách tạm thời xóa đi những cạnh nối $a-b$ hoặc $b-b$ . Ta có hình vẽ $2$ .

Do $G$ có đúng $n-1$ cạnh nên $G$ bị chia thành các thành phần liên thông (cây con), với ví dụ trên ta sẽ tạm gọi các thành phần liên thông (cây con) chỉ chứa đỉnh $a$ là: cây $1$ , cây $3$ và cây $6$ (tương ứng với số đỉnh).

Lúc này, đường đi chỉ có thể thuộc một trong các cây con. Với mỗi cây con, số đỉnh $a$ nhiều nhất có thể đi qua chính là đường kính của cây đó (Các bạn có thể tham khảo định nghĩa, tính chất và thuật toán tìm đường kính tại đây).

Ta dễ dàng có được $k$ bằng độ dài đường kính lớn nhất trong số các cây con. Trong ví dụ trên, $k = 5$ là đường kính của cây $6$ .

Sau khi có được thuật toán cho dạng thứ nhất, ta có thể đưa ra được ý tưởng cho dạng đường đi thứ hai: Kết nối hai cây con thông qua một "khớp nối" là đỉnh $b$ .

Mỗi đỉnh $b$ là "khớp nối" nếu có cạnh nối với $m$ đỉnh $a$ ( $m \geq 2$ ). Vì $G$ có số cạnh $|E| = n - 1$ nên đỉnh $b$ kết nối $m$ cây con. Đường đi dạng thứ hai bao gồm đỉnh $b$ và hai nhánh thuộc hai trong số $m$ cây con.

Trong ví dụ trên, đường đi dạng thứ hai tối ưu nhất có tích số $P = \frac{b}{2+3+1}$ , trong đó có hai đỉnh $a$ thuộc cây con $3$ và ba đỉnh $a$ thuộc cây con $6$ .

Vậy tóm lại, ta cần làm như sau:

Tìm các cây con chỉ chứa đỉnh $a$ .
Tìm đường kính lớn nhất trong số các cây con để tối ưu đường đi dạng thứ nhất.
Duyệt qua với mỗi đỉnh $b$ , tìm hai nhánh có độ dài lớn nhất để tối ưu đường đi dạng thứ hai.

Kết quả là giá trị tích số nhỏ nhất trong hai dạng đường đi.

Độ phức tạp: $\mathcal{O}(n)$ . Code tham khảo

Review in round 1 Câu D

Justinianus posted on June 26, 2023, 6:47 a.m. 1

Tóm tắt đề bài

Tìm bộ ba $x, y, z \geq 0, x + y + z \le S$ sao cho tích $x^a \times y^b \times z^c$ lớn nhất. Giới hạn: $1 \le S \le 1000, 0 \le a, b, c \le 1000$ .

Chúng ta cần tìm cực trị của hàm $f(x, y, z) = x^a \times y^b \times z^c$ theo giới hạn $x + y + z = S$ (kết quả đạt tối đa khi tổng bằng $S$ ) bằng cách sử dụng phương pháp nhân tử Lagrange.

Đặt $L(x, y, z, \lambda) = x^a \times y^b \times z^c + \lambda (x + y + z - S)$ là hàm Lagrange.

Tiếp theo, lấy đạo hàm riêng của $L$ theo $x, y, z$ và $\lambda$ . Đặt các đạo hàm riêng này bằng $0$ sẽ cho chúng ta các giá trị của $x, y, z$ và $\lambda$ tối ưu hóa $f(x, y, z)$ theo ràng buộc $g(x, y, z)$ .

$\displaystyle \begin{cases} \frac{\partial L}{\partial x} = ax^{a-1} \times y^b \times z^c -\lambda = 0 & (1) \\ \frac{\partial L}{\partial y} = ax^a \times y^{b-1} \times z^c -\lambda = 0 & (2) \\ \frac{\partial L}{\partial z} = ax^a \times y^b \times z^{c-1} -\lambda = 0 & (3) \\ \frac{\partial L}{\partial \lambda} = x + y + z - S = 0 & (4) \end{cases}$

Từ ba phương trình $(1) (2) (3)$ , ta có ba vế bằng nhau (cùng bằng $\lambda$ ):

$\lambda = ax^{a-1} \times y^b \times z^c = x^a \times by^{b-1} \times z^c = x^a \times y^b \times cz^{c-1}$

Chia tất cả các vế cho $x^a \times y^b \times z^c$ , ta được mối liên hệ $\frac{a}{x} = \frac{b}{y} = \frac{c}{z}$

Dựa vào mối liên hệ và phương trình $(4)$ ở trên ta có thể thấy tích các lũy thừa đạt giá trị tối đa khi $(x, y, z)$ tỉ lệ với $(a, b, c)$ .

Thu được công thức tính cho từng giá trị $x, y, z$ là:

x = S * a / (a + b + c), y = S * b / (a + b + c), z = S * c / (a + b + c);

Xét riêng trường hợp đặc biệt $a + b + c = 0$ thì kết quả công thức trên trả về giá trị vô định nan do có mẫu số bằng $0$ . Cần phải xử lý riêng bằng việc đặt $x = y = z = 0$ , cho kết quả $x^a \times y^b \times z^c = 0^0 \times 0^0 \times 0^0 = 1 \times 1 \times 1 = 1$ với mọi $S \geq 1$ ( $0^0$ được quy ước có giá trị $1$ trong đại số)

Độ phức tạp thuật toán: $\mathcal{O}(1)$ .

Các bạn có thể tham khảo cài đặt của mình ở mục hướng dẫn giải của bài toán

Review in contest Chào mừng

Yunan posted on June 23, 2023, 1:23 a.m. 0

Tóm tắt đề bài: Cho $N$ món đồ, mỗi món có khối lượng $m_i$ và giá trị $v_i$ . Có $K$ cái túi, mỗi cái túi chứa được tối đa một đồ vật với khối lượng tối đa $c_i$ . Tìm tổng giá trị lớn nhất có thể chọn để bỏ vào túi. Giới hạn: $N,K \le 3.10^5$ .

Nhận xét với dữ kiện “nhiều nhất một món cho một túi”, ta có thể giải quyết bài toán bằng thuật toán tham lam với các tư tưởng như sau:

Đầu tiên ta quan tâm đến những món đồ có giá trị từ cao đến thấp, xem với mỗi món đồ, có tồn tại cái túi nào có thể chứa được hay không.
Để tối ưu, với mỗi món đồ ta phải tìm cái túi có khối lượng nhỏ nhất chứa được.

Với tư tưởng trên, ta đơn giản tiến hành sắp xếp các món đồ theo giá trị tăng (hoặc giảm) của đại lượng $v_i$ . Ta tiến hành duyệt qua với mỗi món đồ, tiếp tục duyệt qua danh sách các cái túi, tìm cái túi có giá trị $c_j$ nhỏ nhất với điều kiện chứa được đồ vật đó $(c_j \geq m_i)$ . Tuy nhiên, độ phức tạp lúc này sẽ là $\mathcal{O}(N.K)$ , dẫn đến TLE.

Vì vây, ta cần tối ưu hóa việc tìm kiếm cái túi phù hợp. Một cách đơn giản nhất ta có thể sử dụng thuật toán tìm kiếm nhị phân: tiến hành sắp xếp $K$ cái túi theo khối lượng, sử dụng tìm kiếm nhị phân để tìm được cái túi nhỏ nhất với $c_j \geq m_i$ . Tuy nhiên, nếu sử dụng mảng, ta sẽ gặp khó trong việc xóa hoặc đánh dấu những cái túi đã được chọn (“nhiều nhất một món cho một túi”).

Các bạn có thể lưu danh sách cái túi với cấu trúc Set để thuận tiện trong việc sắp xếp cũng như xóa các phần tử.

Một lưu ý nhỏ trong việc cài đặt: vì CTDL Set lưu các giá trị khác nhau, vì vậy ta có thể gán nhãn cho các cái túi để biến chúng thành các “bộ giá trị khác nhau ”, cụ thể với mỗi cái túi sẽ có giá trị $m_i$ và nhãn là $i$ .

Độ phức tạp thuật toán: $\mathcal{O}((N \log{} N) + N \log{} K)$ .

Các bạn có thể tham khảo cài đặt của mình ở mục hướng dẫn giải

Hello World!

Review in round 7 Câu D

Review in round 5 Câu D

Review in round 4 Câu E

Review in round 4 Câu D

Review in round 1 Câu C

Review in round 1 Câu D

Review in contest Chào mừng

New problems

Comment stream