Thành phố Konigsberg thuộc Phổ (nay gọi là Kaliningrad thuộc Nga) được chia thành bốn vùng bằng các nhánh sông Pregel. Vào thế kỷ ~18~, người ta xây ~7~ cây cầu nối các vùng này lại với nhau như hình vẽ.

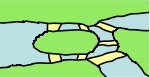
Dân thành phố từng thắc mắc: "Có thể nào đi dạo qua tất cả bảy cây cầu, mỗi cầu chỉ đi qua một lần thôi được hay không?". Ông Euler (1707-1783) chuyển đổi thành bài toán đồ thị như sau: "Có tồn tại hay không một chu trình đơn trong đa đồ thị chứa hết tất cả các cạnh?" và sau đó giải bằng định lý Euler với dấu hiệu nhận biết đồ thị Euler khi và chỉ khi tất cả các đỉnh của đồ thị đều có bậc chẵn với đồ thị vô hướng (có hướng tượng tự khi xét bậc ra/vào trên đỉnh).

Bánh muốn lập trình giải bài toán trên như sau: Cho đa đồ thị vô hướng ~G = (V, E)~, ~V~ được gọi là tập đỉnh và ~|V| = n~, ~E~ được gọi là họ các cạnh của ~G~ và ~|E| = m~. Hãy kiểm tra xem đồ thị trên có phải là đồ thị Euler hay không?

Hãy lập trình giải quyết nội dung trên giúp Bánh.

Input

Dòng thứ nhất chứa hai số nguyên ~n, m~ thỏa ~2 \le n \le 10^2, n - 1 \le m \le (n \times (n + 1))/2~ là số đỉnh và số cạnh của đồ thị.

~m~ dòng kế tiếp biểu diễn cạnh nối giữa hai đỉnh ~x_i, y_i~ của đồ thị thoả ~1 \le x_i, y_i \le n, x_i \neq y_i~.

Output

In ra Yes nếu đồ thị là Euler và No nếu ngược lại.

Samples

Sample Input 1

5 6
2 1
1 3
3 2
1 4
4 5
5 1

Sample Output 1

Yes

Sample Input 2

4 7
2 1
1 2
1 4
2 3
2 3
2 4
3 4

Sample Output 2

No