Xây dựng đồ thị
View as PDF Time limit: 1.0s , Memory limit: 256M , Points: 0 (partial)
Cho đồ thị gồm đỉnh, ban đầu đồ thị không có cạnh nối. Thực hiện
thao tác trên đồ thị như sau:
- Thao tác thứ
(
) gồm ba số nguyên
,
và
(
) : Với mỗi cặp đỉnh
thỏa mãn
, thêm cạnh nối giữa hai đỉnh
và
với độ dài
.
Hỏi sau khi thực hiện tất cả thao tác, độ dài đường đi ngắn nhất từ đỉnh
đến đỉnh
là bao nhiêu ?
Lưu ý rằng đồ thị sau khi thực hiện các thao tác có thể là đa đồ thị.
Input
- Dòng đầu tiên chứa hai số nguyên
và
là số đỉnh và số thao tác (
,
).
dòng tiếp theo, dòng thứ
chứa ba số nguyên
,
và
mô tả thao tác thứ
(
,
).
Output
- In ra độ dài đường đi ngắn nhất từ đỉnh
đến đỉnh
sau khi thực hiện tất cả các thao tác. Nếu không có đường đi từ đỉnh
đến đỉnh
, in ra
.
Examples
Sample Input 1
4 2
1 3 2
3 4 5Sample Output 1
7Sample Input 2
4 2
1 2 2
3 4 1Sample Output 2
-1Scoring
- Subtask
với
số điểm:
- Subtask
với
số điểm:
,
với mọi
- Subtask
với
số điểm:
- Subtask
với
số điểm: Không có ràng buộc gì thêm
Notes
- Ở ví dụ đầu tiên, sau khi thực hiện tất cả các thao tác, đồ thị được xây dựng như sau:
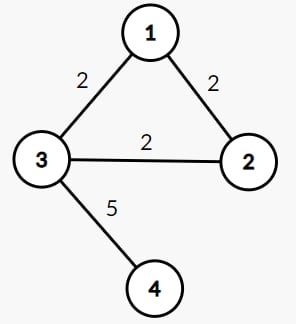
- Ở ví dụ thứ hai, không tồn tại đường đi từ đỉnh
đến đỉnh
trong đồ thị sau:
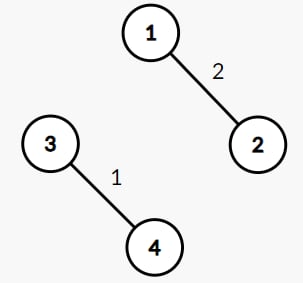
Comments