Phân chia cây

Time limit: 1.0s , Memory limit: 256M , Points: 1500 (partial)

Cho đồ thị dạng cây gồm $N$ ~N~ đỉnh được đánh số từ $1$ ~1~ đến $N$ ~N~. Đỉnh $r$ ~r~ là đỉnh gốc của cây.

Đỉnh $p$ ~p~ được gọi là tổ tiên của đỉnh $u$ ~u~ nếu thỏa mãn cả hai điều kiện:

Có cạnh nối giữa đỉnh $p$ ~p~ và đỉnh $u$ ~u~.
Khi thực hiện duyệt $DFS$ ~DFS~ trên cây, đỉnh $p$ ~p~ được thăm trước đỉnh $u$ ~u~.

Hãy tìm cách phân chia cây thành các đường đi thỏa mãn đồng thời:

Mỗi đỉnh thuộc chính xác một đường đi, một đường đi có thể có một hoặc nhiều đỉnh, các đường đi không nhất thiết phải có cùng số lượng đỉnh.
Mỗi đường đi có dạng $v_1,v_2,...,v_k$ ~v_1,v_2,...,v_k~, trong đó đỉnh $v_i$ ~v_i~ là tổ tiên của đỉnh $v_{i+1}$ ~v_{i+1}~.
Số lượng đường đi là ít nhất.

Ví dụ, cây với $N=5$ ~N=5~ đỉnh và $r=3$ ~r=3~ như hình sau:

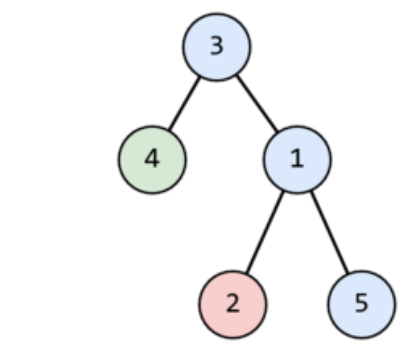
Có thể phân chia cây trên thành $3$ ~3~ đường đi như sau:

Dòng đầu tiên chứa hai số nguyên $N$ ~N~ và $r$ ~r~ $(1 \le N \le 10^5$ ~(1 \le N \le 10^5~ ; $1 \le r \le N)$ ~1 \le r \le N)~.
$N-1$ ~N-1~ dòng tiếp theo, dòng thứ $i$ ~i~ chứa hai số nguyên $u_i$ ~u_i~ và $v_i$ ~v_i~ mô tả cạnh thứ $i$ ~i~ nối hai đỉnh $u_i-v_i$ ~u_i-v_i~ $(1 \le u_i,v_i \le N$ ~(1 \le u_i,v_i \le N~ ; $u_i \neq v_i)$ ~u_i \neq v_i)~.
Dữ liệu đảm bảo đồ thị đã cho là một cây hợp lệ.