Cho đồ thị ~G~ là đơn đồ thị vô hướng, liên thông, có trọng số. Đồ thị ~G~ có tổng cộng ~n~ đỉnh và ~n~ cạnh, các đỉnh được đánh số từ ~1~ đến ~n~ và các cạnh được đánh số từ ~1~ đến ~n~.

Thực hiện thao tác sau đây chính xác một lần:

• Chọn và xóa một cạnh của đồ thị ~G~, thu được đồ thị ~G'~. Lưu ý rằng đồ thị ~G'~ phải là đồ thị liên thông.

Gọi ~d(u,v)~ là độ dài đường đi ngắn nhất giữa hai đỉnh ~u,v~ trong ~G'~.

Gọi ~f(G')~ là giá trị lớn nhất trong số các ~d(u,v)~, hay nói cách khác, ~f(G')=max\{d(u,v)\}~.

Bạn hãy thực hiện thao tác trên sao cho ~f(G')~ đạt giá trị nhỏ nhất.

Input

• Dòng đầu tiên chứa số nguyên ~n~ ~(3 \le n \le 2 \times 10^5)~.
• ~n~ dòng tiếp theo, mỗi dòng chứa ba số nguyên ~u,v,w~ mô tả cạnh nối ~u-v~ có trọng số ~w~ của đồ thị ~(1 \le u,v \le n~ ~;~ ~1 \le w \le 10^9~ ~;~ ~u \neq v)~.
• Dữ liệu đảm bảo đồ thị đã cho là đơn đồ thị liên thông.

Output

• In ra giá trị nhỏ nhất của ~f(G')~.

Examples

Sample Input

4
1 2 7
2 3 5
3 4 1
4 1 3

Sample Output

9

Scoring

• Subtask ~1~ ~-~ ~1500~ điểm: ~n \le 5000~
• Subtask ~2~ ~-~ ~1500~ điểm: Không có ràng buộc gì thêm

Notes

Trong ví dụ, đồ thị ~G~ được mô tả như sau:

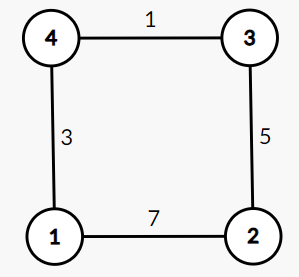
Xét trường hợp xóa cạnh ~1-2~, đồ thị ~G'~ thu được có các giá trị ~d(u,v)~ như sau:

• ~d(1,2)=9~
• ~d(1,3)=4~
• ~d(1,4)=3~
• ~d(2,3)=5~
• ~d(2,4)=6~
• ~d(3,4)=1~

Khi đó, ~f(G') = max\{9,4,3,5,6,1\}=9~.

Xét trường hợp xóa cạnh ~2-3~, đồ thị ~G'~ thu được có ~f(G')=11~.

Xét trường hợp xóa cạnh ~3-4~, đồ thị ~G'~ thu được có ~f(G')=15~.

Xét trường hợp xóa cạnh ~4-1~, đồ thị ~G'~ thu được có ~f(G')=13~.

Vì vậy, ~f(G')~ đạt giá trị nhỏ nhất bằng ~9~.