BFS ???

Time limit: 2.0s , Memory limit: 256M , Points: 2500 (partial)

Cho đơn đồ thị vô hướng, liên thông, không có trọng số bao gồm $2n$ ~2n~ đỉnh, các đỉnh được đánh số từ $0$ ~0~ đến $2n-1$ ~2n-1~. Các cạnh của đồ thị được xây dựng như sau:

Có cạnh nối giữa hai đỉnh $0$ ~0~ và $2n-1$ ~2n-1~ của đồ thị.
Có cạnh nối giữa hai đỉnh $u$ ~u~ và $u+1$ ~u+1~ của đồ thị với mọi $0 \le u < 2n-1$ ~0 \le u < 2n-1~.
Có cạnh nối giữa hai đỉnh $k_i$ ~k_i~ và $k_i+n$ ~k_i+n~ của đồ thị với mọi $1 \le i \le m$ ~1 \le i \le m~.

Vì vậy, đồ thị có tổng cộng $2n+m$ ~2n+m~ cạnh.

Thực hiện $q$ ~q~ truy vấn, với mỗi truy vấn thứ $j$ ~j~ $(1 \le j \le q)$ ~(1 \le j \le q)~, yêu cầu tìm độ dài đường đi ngắn nhất giữa hai đỉnh $x_j$ ~x_j~ và $y_j$ ~y_j~.

Input

Dòng đầu tiên chứa ba số nguyên $n,m,q$ ~n,m,q~ $(2 \le n \le 5 \times 10^8$ ~(2 \le n \le 5 \times 10^8~ $;$ ~;~ $1 \le m \le 5 \times 10^5$ ~1 \le m \le 5 \times 10^5~ $;$ ~;~ $1 \le q \le 2 \times 10^4)$ ~1 \le q \le 2 \times 10^4)~.
Dòng thứ hai chứa $m$ ~m~ số nguyên $k_i$ ~k_i~ $(0 \le k_1 < k_2 < ... < k_m \le n - 1)$ .
$q$ ~q~ dòng tiếp theo, dòng thứ $j$ ~j~ chứa hai số nguyên $x_j$ ~x_j~ và $y_j$ ~y_j~ $(0 \le x_j,y_j \le 2n-1)$ ~(0 \le x_j,y_j \le 2n-1)~.

Output

Với mỗi truy vấn, in ra độ dài đường đi ngắn nhất giữa hai đỉnh $x_j$ ~x_j~ và $y_j$ ~y_j~ trên một dòng.

Examples

Sample Input

Sample Output

2
2
3

Scoring

Subtask $1$ ~1~ $-$ ~-~ $500$ ~500~ điểm: $n,m,q \le 1000$ ~n,m,q \le 1000~
Subtask $2$ ~2~ $-$ ~-~ $750$ ~750~ điểm: $n \le 10^7$ ~n \le 10^7~ $;$ ~;~ $m,q \le 1000$ ~m,q \le 1000~
Subtask $3$ ~3~ $-$ ~-~ $750$ ~750~ điểm: $x_j=0$ ~x_j=0~ với mọi truy vấn
Subtask $4$ ~4~ $-$ ~-~ $500$ ~500~ điểm: Không có ràng buộc gì thêm

Notes

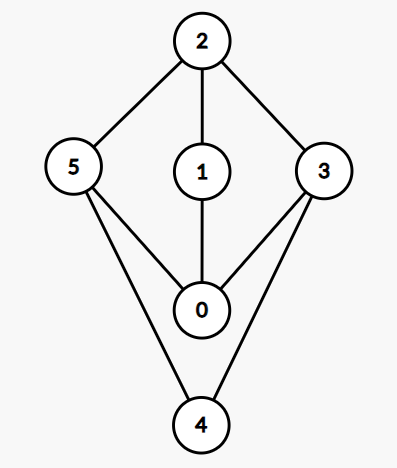
Trong ví dụ, đồ thị được mô tả như trong hình sau: