Chuyến thám hiểm của tiến sĩ Agasa và đội thám tử nhí diễn ra ở thành phố Tokyo. Theo kế hoạch, cả nhóm dự định sẽ đến thăm tổng cộng ~N~ địa điểm, mỗi địa điểm được đánh số phân biệt từ ~1~ đến ~N~. Mỗi địa điểm thứ ~i~ ẩn chứa một báu vật với trọng lượng ~W_i~. Có ~M~ con đường hai chiều nối giữa các địa điểm này, đồng thời xuất phát từ một địa điểm bất kỳ có thể đến được mọi địa điểm khác.

Đội thám tử nhí và tiến sĩ Agasa xuất phát từ thị trấn Beika đến địa điểm thứ nhất, sau đó đến thăm các địa điểm khác. Mỗi khi đến thăm một địa điểm bất kỳ, Mitsuhiko và những người bạn đều muốn mang bảo vật tại địa điểm đó lên xe. Cụ thể, mỗi khi đến thăm địa điểm thứ ~i~ ~(1 \le i \le N)~, trọng lượng của chiếc xe sẽ tăng lên ~W_i~ đơn vị. Đồng thời, để di chuyển qua một con đường bất kỳ, chiếc xe với trọng lượng ~X~ cần đến ~X~ đơn vị nhiên liệu.

Là một người với sở thích đưa ra những câu đố thú vị, tiến sĩ Agasa muốn đội thám tử nhí tính toán rằng với mỗi địa điểm thứ ~i~ ~(1 \le i \le N)~, tổng lượng nhiên liệu ít nhất để di chuyển (tính từ lúc xuất phát) là bao nhiêu. Giả sử rằng khi xuất phát, trọng lượng của xe không đáng kể.

Input

• Dòng đầu tiên chứa hai số nguyên ~N~ và ~M~.
• Dòng thứ hai chứa ~N~ số nguyên ~W_i~ ~(1 \le W_i \le 10^6)~.
• ~M~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~x_i~ và ~y_i~ mô tả cạnh nối giữa hai đỉnh ~(1 \le x_i,y_i \le N)~.
• Dữ liệu đảm bảo xuất phát từ một địa điểm bất kỳ có thể đến được mọi địa điểm khác.

Output

• Với mỗi địa điểm ~i~, in ra trên một dòng là tổng lượng nhiên liệu ít nhất để di chuyển (tính từ lúc xuất phát) để đến được địa điểm đó.

Samples

Sample Input 1

5 6
3 2 2 1 5
1 2
4 2
5 3
1 3
3 2
4 5

Sample Output 1

0
3
3
8
8

Sample Input 2

6 5
1 2 3 4 5 6
1 2
2 3
3 4
4 5
5 6

Sample Output 2

0
1
4
10
20
35

Scoring

• Subtask ~1~ với ~27\%~ số điểm: ~N,M \le 10^6~; ~W_i=W_j~ với mọi ~1 \le i,j \le N~
• Subtask ~2~ với ~19\%~ số điểm: ~N,M \le 10^6~; ~M \le N-1~
• Subtask ~3~ với ~26\%~ số điểm: ~N,M \le 1000~
• Subtask ~4~ với ~28\%~ số điểm: ~N,M \le 5000~

Notes

Trong ví dụ đầu tiên, các địa điểm được minh họa ở hình sau:

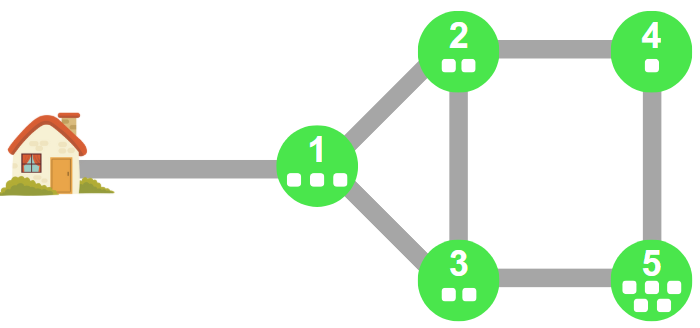
Với điểm đến cuối cùng là địa điểm thứ ~5~, xe xuất phát với trọng lượng bằng ~0~ đến địa điểm thứ nhất, trọng lượng xe tăng lên ~0+3=3~ đơn vị và tiếp tục đến thăm địa điểm thứ ~3~.

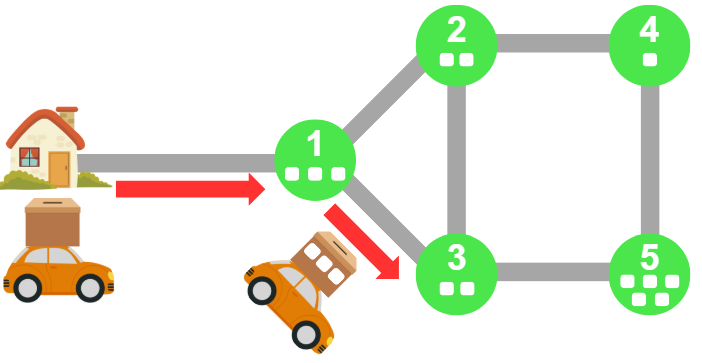
Sau khi đến địa điểm thứ ~3~, trọng lượng xe tăng lên ~3+2=5~ đơn vị và tiếp tục đến địa điểm thứ ~5~.

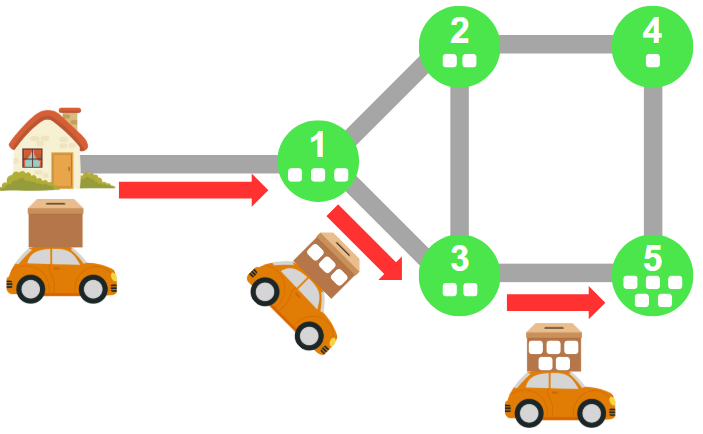
Tổng nhiên liệu cần dùng để từ điểm xuất phát đến địa điểm thứ ~5~ là ~3+5=8~. Có thể nhận thấy rằng không tồn tại cách di chuyển khác có tổng nhiên liệu nhỏ hơn ~8~.