Thang máy

Time limit: 1.0s , Memory limit: 256M , Points: 100 (partial)

Một thang máy được xây dựng tại tòa nhà cao $n$ ~n~ tầng, các tầng được đánh số từ $1$ ~1~ đến $n$ ~n~. Tổng cộng $n$ ~n~ người đang chờ thang máy, người thứ $i$ ~i~ muốn đến tầng thứ $a_i$ ~a_i~. Không có hai người nào muốn đến cùng một tầng, hay nói cách khác, $a$ ~a~ là một dãy hoán vị $n$ ~n~ phần tử.

Thang máy đủ chỗ cho toàn bộ $n$ ~n~ người đứng bên trong, tuy nhiên vì quá hẹp nên tất cả phải đứng xếp hàng dọc theo hướng cửa ra vào. Ban đầu, khi đi vào thang máy ở tầng hầm, người thứ $i$ ~i~ đang đứng ở vị trí $i$ ~i~ tính từ cửa ra vào. Cụ thể, người thứ $1$ ~1~ đứng gần cửa ra vào nhất, người thứ $2$ ~2~ đứng sau người thứ $1$ ~1~, người thứ $3$ ~3~ đứng sau người thứ $2$ ~2~, $...$ ~...~, người thứ $n$ ~n~ đứng sau người thứ $n-1$ ~n-1~ và xa cửa ra vào nhất. Thang máy bắt đầu đi từ tầng hầm đến các tầng thứ $1$ ~1~, $2$ ~2~, $...$ ~...~, $n$ ~n~. Tại mỗi tầng, nếu người thứ $i$ ~i~ muốn đi ra cửa thang máy, tất cả người đứng phía trước người thứ $i$ ~i~ cũng phải đi ra khỏi thang máy. Khi trở lại thang máy, những người đó có thể sắp xếp lại theo thứ tự bất kỳ mà họ muốn. Lưu ý rằng nếu người thứ $i$ ~i~ muốn ra khỏi thang máy, chỉ có những người đứng trước phải đi ra khỏi thang máy, còn những người đứng phía sau người thứ $i$ ~i~ không được ra khỏi thang máy.

Hình sau minh họa thứ tự đứng trong thang máy ở ví dụ đầu tiên:

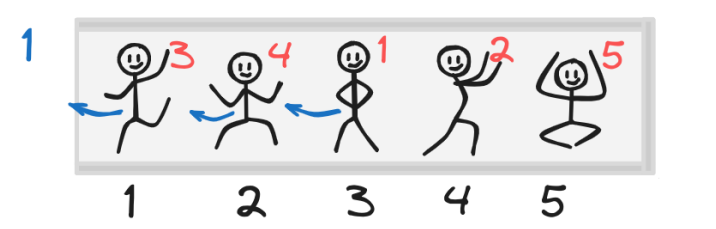
Khi thang máy đến tầng thứ $1$ ~1~, người tại vị trí thứ $3$ ~3~ muốn ra khỏi thang máy, khi đó những người đứng trước bao gồm người tại vị trí thứ $1$ ~1~ và $2$ ~2~ cũng phải rời khỏi thang máy. Lưu ý rằng khi đi vào lại thang máy, hai người này có thể sắp xếp thứ tự đi vào theo cách họ muốn.

Nhiệm vụ của bạn hãy tính tổng số lần đi ra khỏi thang máy ít nhất của tất cả mọi người. Ngoài ra có $q$ ~q~ câu hỏi, câu hỏi thứ $j$ ~j~ yêu cầu xác định rằng nếu người tại các vị trí $x_1,x_2,...,x_j$ ~x_1,x_2,...,x_j~ ban đầu không đi vào thang máy ở tầng hầm (những người còn lại vẫn đứng đúng vị trí và các vị trí $x_1,x_2,...,x_j$ ~x_1,x_2,...,x_j~ được để trống) thì tổng số lần đi ra khỏi thang máy ít nhất của tất cả mọi người là bao nhiêu.

Input

Dòng đầu tiên chứa hai số nguyên $n$ ~n~ và $q$ ~q~ $(0 \le q < n \le 10^5)$ ~(0 \le q < n \le 10^5)~.
Dòng thứ hai $n$ ~n~ số nguyên $a_i$ ~a_i~ $(1 \le a_i \le n)$ ~(1 \le a_i \le n)~.
Dòng thứ ba chứa $q$ ~q~ số nguyên $x_j$ ~x_j~ $(1 \le x_j \le n)$ ~(1 \le x_j \le n)~.

Output

In ra trên một dòng là $q+1$ ~q+1~ số nguyên. Đầu tiên là tổng số lần đi ra khỏi thang máy ít nhất của tất cả mọi người khi chưa có vị trí nào để trống, sau đó là $q$ ~q~ câu trả lời tương ứng với $q$ ~q~ câu hỏi.

Samples

Sample Input 1

5 2
3 4 1 2 5
3 2

Sample Output 1

9 6 4

Sample Input 2

7 0
4 5 2 1 6 3 7

Sample Output 2

Sample Input 3

3 2
3 1 2
1 2

Sample Output 3

5 2 1

Scoring

Subtask $1$ ~1~ với $25\%$ ~25\%~ số điểm: $n,q \le 100$ ~n,q \le 100~
Subtask $2$ ~2~ với $25\%$ ~25\%~ số điểm: $n,q \le 1000$ ~n,q \le 1000~
Subtask $3$ ~3~ với $25\%$ ~25\%~ số điểm: $q=0$ ~q=0~
Subtask $4$ ~4~ với $25\%$ ~25\%~ số điểm: Không có ràng buộc gì thêm

Clarification

Hình sau minh họa cách ra vào thang máy trước câu hỏi đầu tiên (chưa có vị trí nào để trống) ở ví dụ thứ nhất:

Ở tầng thứ $1$ ~1~, người tại vị trí thứ $3$ ~3~ muốn ra khỏi thang máy, khi đó người tại vị trí thứ $1$ ~1~ và $2$ ~2~ cũng phải rời khỏi thang máy, sau đó quay trở lại theo cùng thứ tự.
Ở tầng thứ $2$ ~2~, người tại vị trí thứ $4$ ~4~ muốn ra khỏi thang máy, khi đó người tại vị trí thứ $1$ ~1~ và $2$ ~2~ cũng phải rời khỏi thang máy, sau đó quay trở lại theo cùng thứ tự.
Ở tầng thứ $3$ ~3~, người tại vị trí thứ $1$ ~1~ muốn ra khỏi thang máy, khi đó không còn ai đứng trước.
Ở tầng thứ $4$ ~4~, người tại vị trí thứ $2$ ~2~ muốn ra khỏi thang máy, khi đó không còn ai đứng trước.
Ở tầng thứ $5$ ~5~, người tại vị trí thứ $5$ ~5~ muốn ra khỏi thang máy, khi đó không còn ai đứng trước.

Tổng cộng, người thứ $1,2$ ~1,2~ đều rời thang máy $3$ ~3~ lần và người thứ $3,4,5$ ~3,4,5~ đều rời thang máy $1$ ~1~ lần. Vì vậy tổng số lần đi ra khỏi thang máy ít nhất là $3+3+1+1+1=9$ ~3+3+1+1+1=9~.