Có tổng cộng ~n~ thành phố và ~m~ tuyến xe buýt, mỗi tuyến ~i~ bắt đầu từ thành phố ~a_i~ và kết thúc tại thành phố ~b_i~ với thời gian di chuyển ~t_i~ phút.

Cho một số nguyên ~k~ và ~q~ truy vấn, mỗi truy vấn yêu cầu xác định thời gian ngắn nhất để đi từ thành phố ~c_j~ đến thành phố ~d_j~ nhưng chỉ được sử dụng tối đa ~k~ tuyến xe buýt.

Input

• Dòng đầu tiên chứa hai số nguyên ~n~ và ~m~ ~(2 \le n \le 70; \; 1 \le m \le 10^6)~.
• ~m~ dòng tiếp theo, dòng thứ ~i~ chứa ba số nguyên ~a_i~, ~b_i~ và ~t_i~ ~(1 \le a_i,b_i \le n; \; 1 \le t_i \le 10^6)~ mô tả tuyến xe thứ ~i~.
• Dòng tiếp theo chứa hai số nguyên ~k~ và ~q~ ~(1 \le k \le 10^9; \; 1 \le q \le n^2)~.
• ~q~ dòng tiếp theo, dòng thứ ~j~ chứa hai số nguyên ~c_j~ và ~d_j~ ~(1 \le c_j,d_j \le n)~ mô tả truy vấn.

Output

• Với mỗi truy vấn, in ra trên một dòng là thời gian ngắn nhất để đi từ thành phố ~c_j~ đến thành phố ~d_j~. Nếu không tồn tại đường đi, in ra ~-1~.

Samples

Sample Input 1

4 7
1 2 1
1 4 10
2 3 1
2 4 5
3 2 2
3 4 1
4 3 2
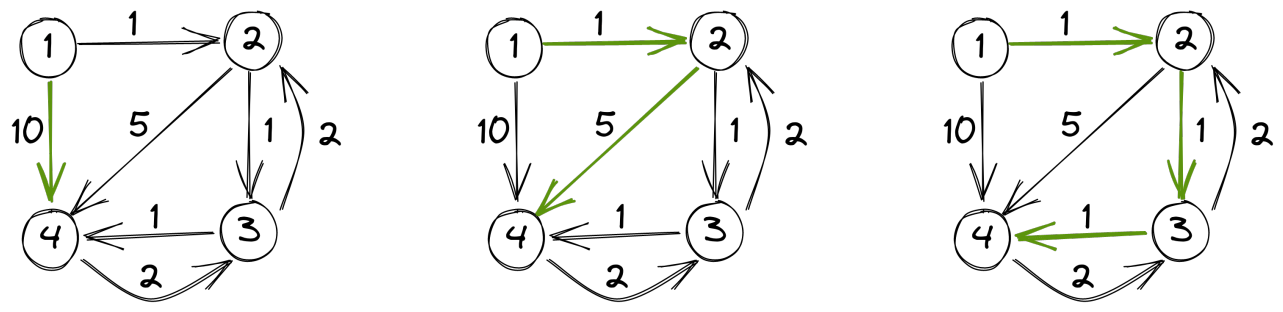
1 3
1 4
4 2
3 3

Sample Output 1

10
-1
0

Sample Input 2

4 7
1 2 1
1 4 10
2 3 1
2 4 5
3 2 2
3 4 1
4 3 2
2 3
1 4
4 2
3 3

Sample Output 2

6
4
0

Sample Input 3

4 7
1 2 1
1 4 10
2 3 1
2 4 5
3 2 2
3 4 1
4 3 2
3 3
1 4
4 2
3 3

Sample Output 3

3
4
0

Scoring

• Subtask ~1~ với ~25\%~ số điểm: ~k \le n \le 7~
• Subtask ~2~ với ~25\%~ số điểm: ~k \le 3~
• Subtask ~3~ với ~25\%~ số điểm: ~k \le n~
• Subtask ~4~ với ~25\%~ số điểm: Không còn ràng buộc gì thêm

Clarification

Hình sau minh họa truy vấn đầu tiên ở các ví dụ. Đường đi ngắn nhất được ký hiệu màu xanh.