Mở rộng cạnh

Time limit: 4.0s , Memory limit: 512M , Points: 100 (partial)

Cho đồ thị gồm $n$ ~n~ đỉnh $1,2,...,n$ ~1,2,...,n~ và $m$ ~m~ cạnh hai chiều có trọng số. Hãy đếm số cạnh thỏa mãn khi mở rộng cạnh đó thêm $2$ ~2~ đơn vị thì độ dài đường đi ngắn nhất từ đỉnh $1$ ~1~ đến đỉnh $n$ ~n~ tăng thêm $1$ ~1~ đơn vị.

Input

Dòng đầu tiên chứa một số nguyên $t$ ~t~ là số lượng test case $(1 \le t \le 10^4)$ ~(1 \le t \le 10^4)~.
Mỗi test case bao gồm dòng đầu tiên chứa hai số nguyên $n$ ~n~ và $m$ ~m~ $(2 \le n \le 3.10^5; \; 1 \le m \le \min(3.10^5, \frac{n(n-1)}{2}))$ .
$m$ ~m~ dòng tiếp theo, mỗi dòng bao gồm ba số nguyên $u$ ~u~, $v$ ~v~ và $w$ ~w~ $(1 \le u,v \le n; \; u \neq v; \; 1 \le w \le 10^9)$ biểu thị cạnh nối hai đỉnh $u$ ~u~ và $v$ ~v~ có độ dài $w$ ~w~. Giữa hai đỉnh bất kỳ có tối đa một cạnh nối giữa chúng, đồng thời xuất phát từ một đỉnh bất kỳ có thể đến mọi đỉnh còn lại.
Dữ liệu đảm bảo tổng $n$ ~n~ của các test case không vượt quá $3.10^5$ ~3.10^5~ và tổng $m$ ~m~ của các test case không vượt quá $3.10^5$ ~3.10^5~.

Output

Với mỗi test case, dòng đầu tiên in ra số nguyên $k$ ~k~ là số lượng cạnh thỏa mãn. Dòng thứ hai in ra các chỉ số của cạnh thỏa mãn theo thứ tự tăng dần, các chỉ số cạnh được đánh số từ $1$ ~1~.

Samples

Sample Input

Sample Output

Scoring

Subtask $1$ ~1~ với $30\%$ ~30\%~ số điểm: $n,m \le 1000$ ~n,m \le 1000~
Subtask $2$ ~2~ với $30\%$ ~30\%~ số điểm: Giữa hai đỉnh $1$ ~1~ và $n$ ~n~ có cạnh nối với độ dài lớn hơn $1$ ~1~ đơn vị so với đường đi ngắn nhất giữa hai đỉnh này.
Subtask $3$ ~3~ với $40\%$ ~40\%~ số điểm: Không còn ràng buộc gì thêm

Clarification

Hình sau minh họa đồ thị trong test case đầu tiên:

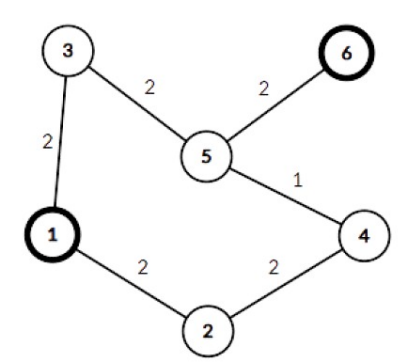
Mở rộng cạnh số $2$ ~2~ (nối đỉnh $1-3$ ~1-3~) hoặc cạnh số $4$ ~4~ (nối đỉnh $3-5$ ~3-5~) sẽ làm tăng độ dài đường đi ngắn nhất từ đỉnh $1$ ~1~ đến đỉnh $n$ ~n~ thêm $1$ ~1~ đơn vị.