Tóm tắt bài toán:

• Cho một cây bao gồm ~n~ đỉnh và ~n - 1~ cạnh. Đếm số lượng đường đi dài nhất trên cây đã cho.

Nhận xét:

• Chọn một đỉnh bất kỳ để làm gốc của cây.
• Xét đỉnh ~u~ và cây con gốc ~u~:
  • Xét một đỉnh ~v~ bất kỳ nằm trong cây con gốc ~u~, tập các đường đi ~P_u~ bắt đầu từ đỉnh ~u~ sẽ bao gồm đường đi ~u - v~.
  • Xét hai đỉnh ~v1~, ~v2~ bất kỳ nằm ở hai nhánh khác nhau của cây con gốc ~u~, tập các đường đi ~P_u~ đi qua ~u~ sẽ bao gồm đường đi ~v1 - u - v2~.
• Tập tất cả các đường đi trong cây ban đầu là hợp của tất cả tập các đường đi ~P_i~ chứa đỉnh ~i~ trong cây con gốc ~i~.
• Và ~P_i \cap P_j = \varnothing~ với ~i \neq j~, tức hai tập đường đi bất kỳ không chứa hai đường đi giống nhau.

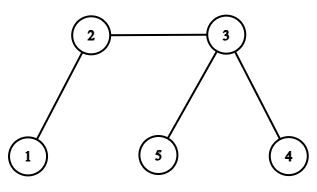
• Như trong hình trên, giả sử ta chọn đỉnh ~1~ là đỉnh gốc của cây.
  • Tập các đường đi ~P_1~ chứa đỉnh ~1~ trong cây con gốc ~1~ là:
    • ~1~.
    • ~1 - 2~.
    • ~1 - 2 - 3~.
    • ~1 - 2 - 3 - 5~.
    • ~1 - 2 - 3 - 4~.
  • Tập các đường đi ~P_2~ chứa đỉnh ~2~ trong cây con gốc ~2~ là:
    • ~2~.
    • ~2 - 3~.
    • ~2 - 3 - 5~.
    • ~2 - 3 - 4~.
  • Tập các đường đi ~P_3~ chứa đỉnh ~3~ trong cây con gốc ~3~ là:
    • ~3~.
    • ~3 - 5~.
    • ~3 - 4~.
    • ~4 - 3 - 5~.
  • Tập các đường đi ~P_4~ chứa đỉnh ~4~ trong cây con gốc ~4~ là:
    • ~4~.
  • Tập các đường đi ~P_5~ chứa đỉnh ~5~ trong cây con gốc ~5~ là:
    • ~5~.
• Tập tất cả đường đi trên cây ban đầu là hợp của tất cả tập các đường trên, tức là ~P_1 \cup P_2 \cup P_3 \cup P_4 \cup P_5~.
• Và ~P_i \cap P_j = \varnothing~ với ~1 \le i \neq j \le 5~.

Thuật toán:

• Từ nhận xét trên, ta chỉ cần đếm số lượng đường đi dài nhất trong các tập ~P_i~.
• Để thực hiện bài toán trên, ta sử dụng kỹ thuật quy hoạch động trên cây như sau:
  • Gọi ~maxDepth_u~ là độ sâu tối đa của cây con gốc ~u~ và ~cntMaxDepth_u~ là số lượng đường đi bắt đầu từ đỉnh ~u~ trong ~P_u~ có độ dài bằng ~maxDepth_u~.
  • Ta có thể tính các giá trị ~maxDepth_u~ và ~cntMaxDepth_u~ bằng DFS trong độ phức tạp ~O(n)~.
  • Với mỗi đỉnh ~u~:
    • Nếu ~u~ chỉ có một nhánh thì độ dài và số lượng đường đi dài nhất trong ~P_u~ là ~maxDepth_u~ và ~cntMaxDepth_u~.
    • Nếu ~u~ có hai nhánh trở lên thì độ dài đường đi dài nhất trong ~P_u~ là ~max(maxDepth_{v1} + maxDepth_{v2} + 2)~ với ~v_1~, ~v_2~ là hai đỉnh con trực tiếp bất kỳ của ~u~. Với trường hợp này, ta có thể tính toán độ dài và số lượng đường đi dài nhất trong độ phức tạp ~O(k*log(k))~ hoặc ~O(k)~ với ~k~ là số lượng đỉnh con trực tiếp của ~u~.
• Độ phức tạp: ~O(n)~ hoặc ~O(n*log(n))~.