Trong một đồ thị dạng cây, khoảng cách giữa hai đỉnh bất kỳ được định nghĩa là số cạnh nằm trên đường đi nối hai đỉnh đó. Đường kính của cây là khoảng cách lớn nhất trong tất cả các cặp đỉnh. Một cây được gọi là cân đối với hệ số ~K~ nếu đường kính của cây đó không vượt quá ~K~.

Cho một cây gồm ~N~ đỉnh (các đỉnh được đánh số từ ~1~ đến ~N~). Nhiệm vụ của bạn hãy xóa một số lượng ít nhất (có thể không xóa) các đỉnh để cây trở nên cân đối với hệ số ~K~. Khi xóa một đỉnh, các cạnh nối đỉnh đó cũng được xóa theo.

Lưu ý rằng các đỉnh và các cạnh còn lại sau khi xóa phải tạo thành một cây hợp lệ.

Input

• Dòng đầu tiên chứa hai số nguyên dương ~N~ và ~K~ là số lượng đỉnh của cây và hệ số cân đối (~2 \leq N \leq 2000~, ~1 \le K \leq N~).
• ~N-1~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~u_i~ và ~v_i~ mô tả cạnh nối giữa hai đỉnh ~u_i~ và ~v_i~ (~1 \le u_i,v_i \le N~).
• Dữ liệu đảm bảo các cạnh nối tạo thành một cây hợp lệ.

Output

• In ra một số nguyên là số lượng ít nhất các đỉnh cần xóa để tạo thành một cây cân đối.

Examples

Sample Input 1

6 2
5 2
2 1
5 3
4 5
5 6

Sample Output 1

1

Sample Input 2

3 2
2 3
3 1

Sample Output 2

0

Scoring

• Subtask ~1~ với ~50\%~ số điểm: ~N \le 10~
• Subtask ~2~ với ~50\%~ số điểm: ~N \le 2000~

Notes

• Hình bên dưới mô tả cây trong ví dụ thứ nhất. Cây sau khi xóa đỉnh ~1~ có đường kính là ~2~.

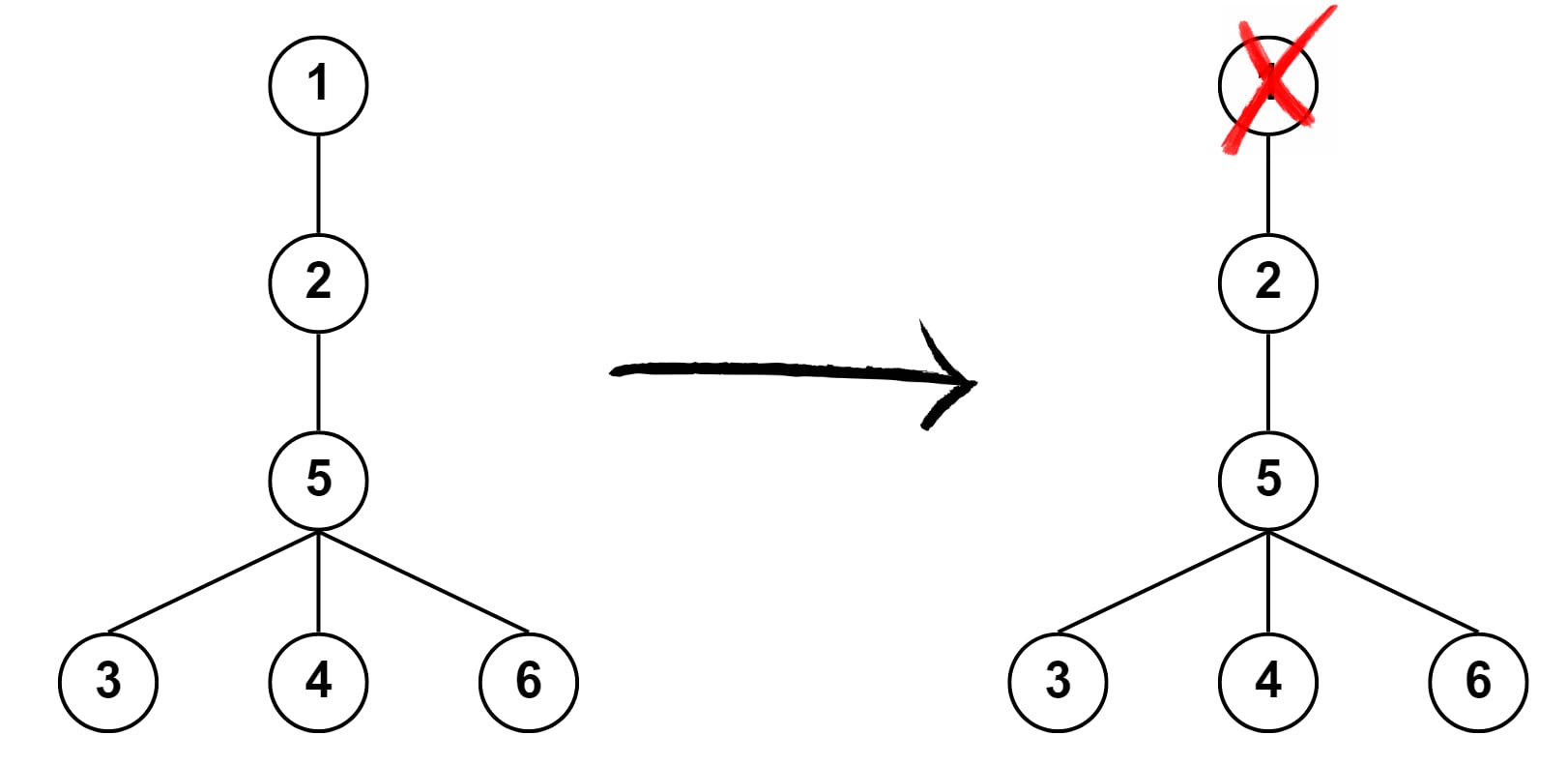
• Ở ví dụ thứ hai, lưu ý rằng có thể không thực hiện thao tác xóa đỉnh nào.