Trung tâm của cây (Center of Tree) được định nghĩa là đỉnh (trong trường hợp đường kính là số chẵn) hoặc cạnh (trong trường hợp đường kính là số lẻ) nằm chính giữa trên đường nối dài nhất giữa hai đỉnh của cây. Trong hình sau, đỉnh hoặc cạnh được tô màu xanh là trung tâm của cây:

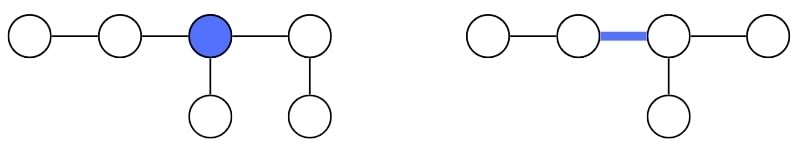
Dễ dàng thấy rằng, với ~D~ là đường kính của cây, khi đó khoảng cách tối đa từ trung tâm của cây đến một đỉnh bất kỳ là ~\lfloor\frac{D}{2}\rfloor~. Từ đó, ta có phương pháp giải quyết bài toán này như sau:

• Với ~K~ chẵn, xét với mỗi đỉnh ~i~ (~1 \le i \le N~), chọn đỉnh ~i~ làm trung tâm của cây. Tiến hành đếm số lượng đỉnh cần xóa bằng cách tính khoảng cách từ đỉnh trung tâm đến tất cả các đỉnh khác (đỉnh cần xóa có khoảng cách đến đỉnh trung tâm lớn hơn ~\frac{D}{2}~).
• Với ~K~ lẻ, xét với mỗi cạnh ~i~ (~1 \le i \le N-1~), chọn cạnh ~i~ làm trung tâm của cây. Tiến hành đếm số lượng đỉnh cần xóa bằng cách tính khoảng cách từ cạnh trung tâm đến tất cả các đỉnh khác (đỉnh cần xóa có khoảng cách đến cạnh trung tâm lớn hơn ~\lfloor \frac{D}{2} \rfloor~).

Đáp án của bài toán là số lượng đỉnh cần xóa ít nhất trong số các cách chọn đỉnh hoặc cạnh trung tâm.

Độ phức tạp: ~O(N^2)~